平方式の作り方

平方式と完全平方式と平方完成が何なのかは分かった。

平方式はどうやって作るの？

平方式というのは、

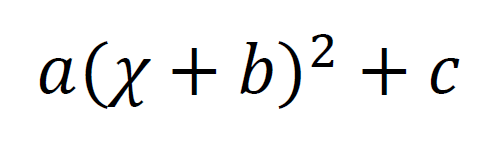
こういう感じの式。

今からこんな感じの平方式を作る。

まず、2乗のペアの式を作る。

こういうの。

ここから、2種類の平方式を作ることができる。

プラス

まずはプラスの方。

と、

こうなる。

式を整理すると、

となるので、因数分解の公式１．を使って、

こんな感じに因数分解できる。

ここから、加えたものを除く。

つまり、式で書くと、

(　)外すと、

これで平方式の形になった。

プラスはこんな感じ。

マイナス

次にマイナス。

やることはほぼ同じ。

と、

こうなる。

式を整理すると、

となるので、因数分解の公式１．を使って、

こんな感じに因数分解できる。

ここから、加えたものを除く。

つまり、式で書くと、

(　)外すと、

これで平方式の形になった。

マイナスはこんな感じ。

プラスとマイナスを並べてみると、

こんな感じ。

どう使うの？

じゃあ具体的にどうやって因数分解で使うのか。

こんな問題が来た時に平方式を使う。

この式を因数分解する。

4乗…

4乗て…

と、触りたくなくなるような式。

でもここで、「16は4の2乗」というところに注目。

少し式を入れ替えると、

ここで！

平方式に変形！

を使って、少し計算すると、

って感じで、因数分解ができるプラスの方の平方式に変形させる。

同類項をまとめると、

こんな感じになる。

ここでまた因数分解の公式を使いたいけど、ややこしいから分かりやすく置き換える。

因数分解の公式２．を使って、

ここまで因数分解して、置き換えた文字を元の形に戻す。

これで一応因数分解できた。

これでも正解。

すこし整理すると、

これが割ときれいな形。

どっちでも正解。

定義を知る

平方式の作り方

まとめ

平方式に変形させて因数分解して解く問題は、問題自体に結構特徴がある。

似たような問題を解いて、平方完成をすることに慣れておけば、

グラフを書くとき、式を変形させることが苦じゃなくなる。

「二次関数のグラフ」で役立ちますように。