ルートの整数部分と小数部分

ルートを整数部分と小数部分に分けて計算するとき、
数直線をイメージすると分かりやすい。

とりあえず、プラス方向の「ルート」を考える。

数直線上のルートの配置がこんな感じ。
なんか最後の方すごく窮屈になってる…。

整数部分と小数部分とは

それぞれ整数部分と小数部分がある。

こんな感じ。
【整数部分】＋【小数部分】で構成されている。

整数部分の判断

例えば、

これらの数の【整数部分】と【小数部分】が何かを考える。
もう一度数直線を見てみると、

こんな感じの位置にいらっしゃる。
ここで、何の整数の間にいるかを考える。
いきなり何の整数の間にいるかを考えるんじゃなくて、
整数になるルートが何なのかをまず考えてから整数に直す。
すると、

こんな感じになるから、それを踏まえてそれぞれの【整数部分】は、

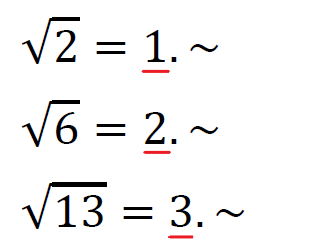
こんな感じになる。
これが整数部分。

小数部分の判断

次は【小数部分】を考える。
小数部分は、整数部分を引くと出てくる。
つまり、

こんな感じになる。
これが小数部分。

発展

もう少し発展させる。

分母にルートがあるから、まずは分母の有利化をする。

こんな感じに、分数の形になる。
まずは、整数部分が何かを考える。

これで√2の整数部分が「１」ということが分かった。
ここで問題なのが、求める数の整数部分は、
分母が「２」だから、分子が2の倍数にならないと整数にならないということ。
「２＋１．～」だと「４」には届かない。
なので、

こんな感じに、整数部分を求めることができる。

次に、小数部分が何かを考える。
小数部分は、整数部分を引くと出てくる。

こんな感じに小数部分を求めることができる。

定義を知る

まずは、「整数部分」「小数部分」が何なのかを知る。

まとめ

まずは【整数部分】、「何の整数の間にいるか」を考える。
それから【小数部分】、「整数部分を引く」。
分数のときは分母の倍数が分子になる時が整数部分になる。